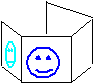
Το ζητούμενο είναι να κατασκευάσετε μια "τρύπα" σε έναν κύβο, αρκετά μεγάλη ώστε να χωράει να περάσει μέσα από αυτήν ένας κύβος του ίδιου μεγέθους.
Όχι... δεν αστειευόμαστε! Είναι κάτι που γίνεται, μάλιστα το πρόβλημα αυτό έχει πριγκιπική προέλευση. Το έθεσε ο πρίγκιπας Rupert (1619-1682), πρώτος ανηψιός του βασιλιά Καρόλου του 1ου της Αγγλίας και πρώτος θείος του Γεωργίου του 1ου της Μεγάλης Βρετανίας. Αναφέρεται πως εκτός από καλός στρατηγός και πολεμιστής ήταν φιλομαθής, ασχολήθηκε με τις επιστήμες και τις τέχνες.
Ας δούμε λοιπόν την ενδιαφέρουσα λύση στο πρόβλημά του: Θεωρούμε έναν άξονα που διέρχεται από δύο κορυφές του κύβου που δεν είναι στην ίδια έδρα. Αυτός ο άξονας διέρχεται από το κέντρο του και μάλιστα, αν τμήσουμε το κύβο με επίπεδο κάθετο στον άξονα αυτό που να διέρχεται από το κέντρο του θα προκύψει ένα κανονικό εξάγωνο με πλευρά a√2/2, όπου a είναι η ακμή του κύβου. Το μέγεθος αυτού του εξαγώνου είναι αρκετά μεγάλο, ώστε να "χωράει" ένα τετράγωνο πλευράς a στο εσωτερικό του. Συνεπώς, η "ζητούμενη τρύπα" είναι κάπως έτσι:
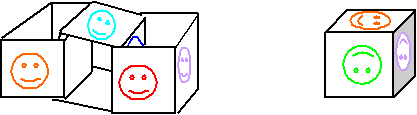
Και εδώ είναι το επιτυχές πέρασμα:
Μπορείτε να κατασκευάσετε κι εσείς τους δύο κύβους με τη βοήθεια του προτύπου που δημιούργησε ο Martin Raynsford.
Dürer's Magic Square, Cardano's Rings, Prince Rupert's Cube, and Other Neat Things, V. Frederick Rickey
Prince Rupert of the Rhine - Wikipedia
Όχι... δεν αστειευόμαστε! Είναι κάτι που γίνεται, μάλιστα το πρόβλημα αυτό έχει πριγκιπική προέλευση. Το έθεσε ο πρίγκιπας Rupert (1619-1682), πρώτος ανηψιός του βασιλιά Καρόλου του 1ου της Αγγλίας και πρώτος θείος του Γεωργίου του 1ου της Μεγάλης Βρετανίας. Αναφέρεται πως εκτός από καλός στρατηγός και πολεμιστής ήταν φιλομαθής, ασχολήθηκε με τις επιστήμες και τις τέχνες.
Ας δούμε λοιπόν την ενδιαφέρουσα λύση στο πρόβλημά του: Θεωρούμε έναν άξονα που διέρχεται από δύο κορυφές του κύβου που δεν είναι στην ίδια έδρα. Αυτός ο άξονας διέρχεται από το κέντρο του και μάλιστα, αν τμήσουμε το κύβο με επίπεδο κάθετο στον άξονα αυτό που να διέρχεται από το κέντρο του θα προκύψει ένα κανονικό εξάγωνο με πλευρά a√2/2, όπου a είναι η ακμή του κύβου. Το μέγεθος αυτού του εξαγώνου είναι αρκετά μεγάλο, ώστε να "χωράει" ένα τετράγωνο πλευράς a στο εσωτερικό του. Συνεπώς, η "ζητούμενη τρύπα" είναι κάπως έτσι:
Και εδώ είναι το επιτυχές πέρασμα:
Μπορείτε να κατασκευάσετε κι εσείς τους δύο κύβους με τη βοήθεια του προτύπου που δημιούργησε ο Martin Raynsford.
Πηγές
Math Monday - Passing a Cube Through Another Cube - The Museum of MathematicsDürer's Magic Square, Cardano's Rings, Prince Rupert's Cube, and Other Neat Things, V. Frederick Rickey
Prince Rupert of the Rhine - Wikipedia